Jan 2025 Jane Street Puzzle Write-up
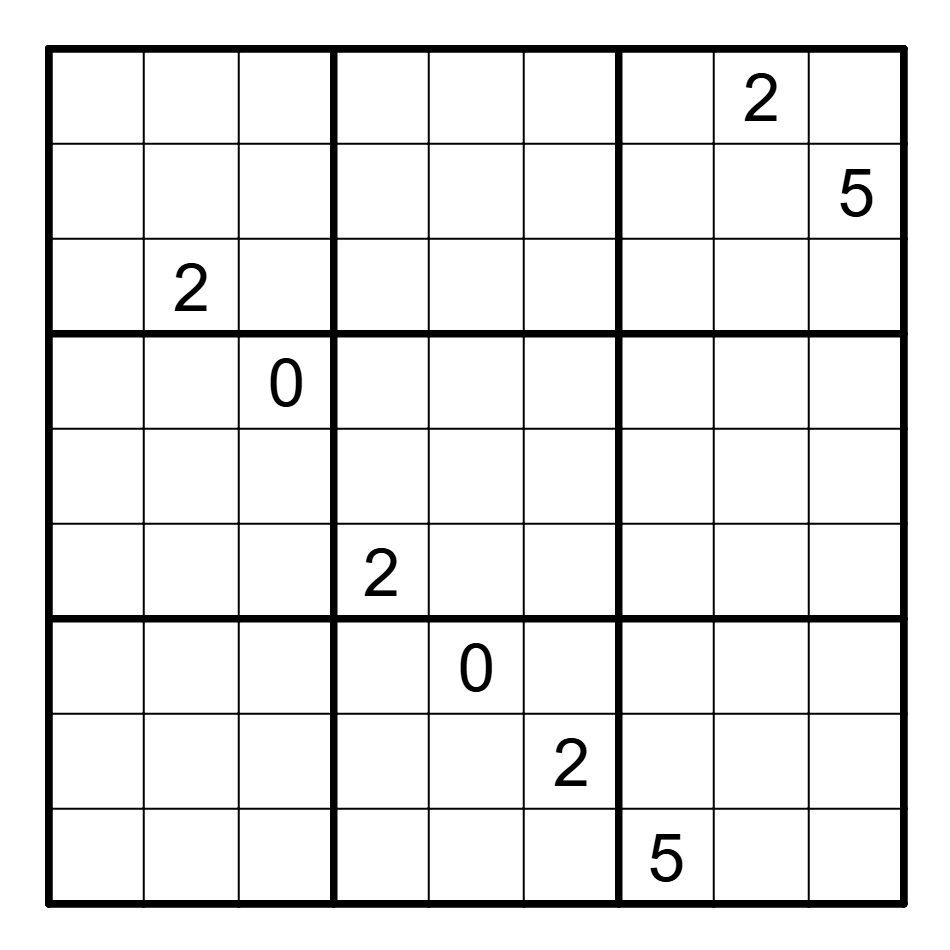
This month's puzzle asks us to find a valid solution to a Sudoku grid (shown above) with some special constraints. Here's the puzzle description:
Fill the empty cells in the grid above with digits such that each row, column, and outlined 3-by-3 box contains the same set of nine unique digits[1], and such that the nine 9-digit numbers[2] formed by the rows of the grid has the highest-possible GCD over any such grid.
Some of the cells have already been filled in. The answer to this puzzle is the 9-digit number formed by the middle row in the completed grid.
[1] that is, you’ll be using nine of the ten digits (0-9) in completing this grid
[2] possibly with a leading 0
This is the classic constraint satisfaction problem of Sudoku with some additional rules—to break down the problem, we need to find a grid configuration such that:
- the grid uses nine unique digits $\mathcal{D}$;
- the grid satisfies normal Sudoku rules; and
- the nine-digit numbers formed by the rows of the grid $r_1, r_2, \dots, r_9$ are such that $\mathrm{gcd}(r_1,r_2,\dots, r_9)=\max\left\{\mathrm{gcd}(r^{(1)}_1,r^{(1)}_2,\dots,r^{(1)}_9), \mathrm{gcd}(r^{(2)}_1,r^{(2)}_2,\dots,r^{(2)}_9), \dots\right\}$ where $r^{(j)}_i$ is the $i$-th row number of the $j$-th valid grid configuration that satisfies (1) and (2).
Toward a solution¶
You may have realized that due to the number of valid solutions for the given grid, brute-forcing all possible solutions is not feasible. Instead, we need to examine the properties of the puzzle (i.e., the nine-digit numbers and the greatest common divisor) to see if we can narrow the search space.
A useful property of the greatest common divisor¶
Loosely defined, the greatest common divisor (GCD) of two or more integers is the largest (positive) integer value that divides the numbers with no remainder. For example, 10 and 15 have $\mathrm{gcd}(10,15)=5$ since 5 is the largest integer that exactly divides both 10 and 15.
If $a$ and $b$ have a GCD of $n$, then we can express $a$ and $b$ in terms of multiples of $n$, i.e., $a=n\cdot p$ and $b=n\cdot q$, where $p,q$ are both (positive) integers. If we add $a$ and $b$, then we have $a+b=n\cdot p + n\cdot q = n(p+q)$. Since $n$, $p$, and $q$ are all integers, this tells us that the GCD $n$ also exactly divides $a+b$. Situating this in the context of the puzzle, if $n$ is the GCD of the row numbers $r_1, r_2, \dots$, then we also know $n$ must be a divisor of the sum of the row numbers $\sum_i r_i$.
Therefore, if we knew the possible sums of row numbers across valid Sudoku grids, we'd know the true GCD would be a divisor (factor) of one the sums, and we could use these factors to generate row number candidates to search for a solution faster.
Potential sums of row numbers¶
Re-examining constraint (1), we know that the grid must use nine of the ten digits between 0–9. Since the grid already contains 0, 2, and 5, we know that we must choose one of 1, 3, 4, 6, 7, 8, or 9 to exclude. This leaves us with seven possible sets of nine unique digits $\mathcal{D}$ to choose from.
The key realization to make here is that due to the Latin square property, simply knowing which digits are used in the grid is enough to find the sum of the row numbers. Since we know every column must contain each digit in $\mathcal{D}$ exactly once, the sum of each column is therefore the sum of the digits $\sum_{d\in \mathcal{D}} d$.
Depending on the column, we can multiply by a power of 10 to account for its units:
$$ \sum_i r_i =10^0\sum_{d\in \mathcal{D}} d + 10^1\sum_{d\in \mathcal{D}} d + \cdots + 10^8\sum_{d\in \mathcal{D}} d $$or more simply, $\sum_i r_i = 111,111,111 \cdot \sum_{d\in \mathcal{D}} d$.
We can generate the possible sums for each excluded digit via some Python:
sums = {
d: 111_111_111 *
np.sum([n for n in range(10) if n != d])
for d in [1, 3, 4, 6, 7, 8, 9]
}
for d, s in sums.items(): print(f"Exclude {d}: {s}")
We can factorize these potential sums to deduce that there are 186 GCD candidates to choose from:
def factors(x):
factors = set()
for i in range(1, int(np.sqrt(x)) + 1):
if x % i == 0:
factors.add(i)
factors.add(x // i)
return sorted(factors)
all_factors = sorted(
set(
[ # comprehension to flatten nested list
factor for factors in
[factors(s) for s in sums.values()]
for factor in factors
]
)
)
print(f"{len(all_factors)} factors are: {all_factors}")
And now we're ready to implement an algorithm to check for valid solutions given a GCD candidate. Since we want the maximum satisfying GCD, we'll feed the algorithm the largest candidate first (i.e., reverse the above sorted list).
Puzzle implementation¶
I used Prolog to solve this month's puzzle since it has great support for solving constraint satisfaction problems—you can view the full file here. The main interface of the puzzle looks like so:
% solve_puzzle/2 binds a grid G and GCD with a solution satisfying the puzzle
solve_puzzle(G, GCD) :-
candidates(SortedCandidates),
solve_puzzle_aux(G, SortedCandidates, GCD).
% auxiliary predicate for solve_puzzle--iteratively tries GCD candidates until
% a valid solution is found
solve_puzzle_aux(G, [Factor-Digit|T], GCD) :-
puzzle(G),
( valid_sol(G, Digit, Factor) ->
GCD = Factor, !
; solve_puzzle_aux(G, T, GCD)
).
In the first predicate, we generate all candidate factors and call an auxiliary function to try to find a valid solution to the Sudoku grid given the Factor and excluded Digit (in key-value pair format). If we find a solution, we halt (return); otherwise, we try the next largest candidate (the (X -> Y ; Z) syntax in Prolog is if-then-else).
Generating and sorting the candidates is relatively easy—we can reuse work from above to create seven factors(ExcludedDigit, Factors) predicates that list the factors for a given excluded digit:
for d, s in sums.items():
print(f"factors({d}, {factors(s)}).")
And incorporate this into a predicate to generate the candidates in order to attempt:
% candidates/1 binds ordered Candidates in key-value format where the key is
% the factor and the value is the deleted digit
candidates(Candidates) :-
findall(
Factor-DelDigit,
(
factors(DelDigit, Factors),
member(Factor, Factors)
),
AllCandidates
),
keysort(AllCandidates, SortedCandidates), % this sorts candidates by factors
reverse(SortedCandidates, Candidates). % ...and this reverses the order
Now we can define valid_sol(Grid, DelDigit, GCD), which takes in a Sudoku grid to solve, an excluded digit, and GCD candidate to check if the cells in Grid can be filled satisfying the constraints of the puzzle. I used the CLP(FD) library and based my predicate on an existing Sudoku example.
First, we ensure the shape of the grid is 9x9:
% predicate to solve puzzle given a grid, excluded digit, and a GCD
valid_sol(Grid, DelDigit, GCD) :-
% valid sudoku shape
length(Grid, 9),
maplist(same_length(Grid), Grid),
append(Grid, AllCells),
Then, we need to ensure all but one of the digits 0–9 are used:
% puzzle uses digits 0-9 except one
AllCells ins 0..9,
member(DelDigit, [1,3,4,6,7,8,9]),
maplist(clpfd_ne(DelDigit), AllCells), % we'll define `clpfd_ne` later
Next, we state the last two constraints for Sudoku: Each row, column, and 3x3 box contain exactly one of the used digits:
% all rows & columns have distinct digits
maplist(all_distinct, Grid),
transpose(Grid, Cols), maplist(all_distinct, Cols),
% sudoku boxes
Grid = [As,Bs,Cs,Ds,Es,Fs,Gs,Hs,Is],
blocks(As, Bs, Cs),
blocks(Ds, Es, Fs),
blocks(Gs, Hs, Is),
Finally, we need to add the main puzzle constraint: The provided GCD must exactly divide each of row-wise numbers (since we'll use this predicate to test GCD candidates from largest to smallest, the first satisfying GCD candidate we find is our answer):
% puzzle constraint: GCD divides each row-wise number
maplist(list_to_integer, Grid, RowNumbers),
maplist(is_divisible(GCD), RowNumbers),
maplist(label, Grid).
That's it for the main predicate—now we need to define the rest of the helper predicates: The blocks/3 predicate ensures that 3x3 boxes in the Sudoku grid contain all unique digits:
% helper predicate for boxes
blocks([], [], []).
blocks([N1,N2,N3|Ns1], [N4,N5,N6|Ns2], [N7,N8,N9|Ns3]) :-
all_distinct([N1,N2,N3,N4,N5,N6,N7,N8,N9]),
blocks(Ns1, Ns2, Ns3).
Next, I define two predicates for convenience: clpfd_ne/2 lets me maplist over the grid's cells to assert no cell is equal to our excluded digit, and is_divisible/2 allows for a similar mapping when checking GCD divisibility.
% custom CLPFD predicate for inequality
clpfd_ne(A, B) :- A #\= B.
% flipped predicate for divisibility
is_divisible(B, A) :- A mod B #= 0.
Finally, the list_to_integer/2 predicate converts a row of cells to a nine-digit number:
% predicate to convert list of digits to integer
list_to_integer([], 0).
list_to_integer([Digit|Rest], Number) :-
list_to_integer(Rest, RestNumber),
length(Rest, Len),
Power #= 10^Len,
Number #= Digit * Power + RestNumber.
And we can encode the puzzle grid as such:
puzzle(Grid) :-
Grid = [
[_, _, _, _, _, _, _, 2, _],
[_, _, _, _, 2, _, _, _, 5], % note that this 2 is implicit in the grid
[_, 2, _, _, _, _, _, _, _],
[_, _, 0, _, _, _, _, _, _],
[_, _, _, _, _, _, _, _, _],
[_, _, _, 2, _, _, _, _, _],
[_, _, _, _, 0, _, _, _, _],
[_, _, _, _, _, 2, _, _, _],
[_, _, _, _, _, _, 5, _, _]
].
Solving the grid¶
We can run our solve_puzzle/2 predicate to solve the puzzle:
?- time(solve_puzzle(G, GCD)), maplist(portray_clause, G).
% 93,516,469 inferences, 4.637 CPU in 4.835 seconds (96% CPU, 20169286 Lips)
[3, 9, 5, 0, 6, 1, 7, 2, 8].
[0, 6, 1, 7, 2, 8, 3, 9, 5].
[7, 2, 8, 3, 9, 5, 0, 6, 1].
[9, 5, 0, 6, 1, 7, 2, 8, 3].
[2, 8, 3, 9, 5, 0, 6, 1, 7].
[6, 1, 7, 2, 8, 3, 9, 5, 0].
[8, 3, 9, 5, 0, 6, 1, 7, 2].
[5, 0, 6, 1, 7, 2, 8, 3, 9].
[1, 7, 2, 8, 3, 9, 5, 0, 6].
G = [[3, 9, 5, 0, 6, 1, 7, 2|...], [0, 6, 1, 7, 2, 8, 3|...], [7, 2, 8, 3, 9, 5|...], [9, 5, 0, 6, 1|...], [2, 8, 3, 9|...], [6, 1, 7|...], [8, 3|...], [5|...], [...|...]],
GCD = 12345679.
Prolog yields a solution in under 5s with a GCD of 12,345,679 (the puzzle answer is the middle row number, or 283,950,617). If we look for the GCD in our list,
all_factors[::-1].index(12345679)
Prolog evidently tried 74 (larger) GCD candidates before identifying the correct one.
Conclusion¶
I think there are two main takeaways from this puzzle: First, if a combinatorial problem is too difficult to brute-force, either you need a guiding heuristic (as in Jun 2024), or you need to deduce additional properties about the problem to narrow your search space (as in this puzzle and May 2024).
Second, if you use a SAT solver engine like I did (Prolog, Z3, etc.), you can't rely on it to do all of the work. Perhaps the most "declarative" solution to this problem would be to enumerate all GCD-grid pairs, sort the list according to GCDs (in non-ascending order), and take the head of the list. However, there is no lazy approach the inference engine can take to deduce the maximum GCD (head of the list) without enumerating all solutions—meaning you're back at the problem of brute force. Therefore, you need to do some "gearing" (in this case, trying largest candidates first) to reap the convenience of the SAT solver while ensuring the program terminates.