Surprising Results from Off-center Measurements of Circles
The radius of a circle is defined as the distance from the circle's center to any point on its circumference. If you move the point of measurement to be off-center (as in the figure above), the distances to the circle's circumference are no longer all equal to the circle's radius. But what if you took the mean all of those individual distances—would you recover the value of the radius?
In this post, I discuss how for any off-center point within a circle:
- averaging the distances from the point to the circle's circumference yields a value strictly larger than the circle's radius; and
- averaging the distances that pass through the chosen point from one side of the circle to the other yields a value strictly smaller than the circle's diameter.
Introduction¶
I was watching a video about a radial planimeter from the 1920s, used to approximate the "average radius" of a circular shape, when I heard something that surprised me:
It's a strange — but true — fact that the average radius as measured from the center of a circle is different from the average if you measure it off-center [...]
I thought this was odd, since my intuition was that circular symmetry would account for the loss in distance to the circumference in one length with the longer corresponding opposite length. Unable to convince myself with some mental geometry, I set out to understand this odd fact a little better.
The average off-center radius is always larger than the true radius¶
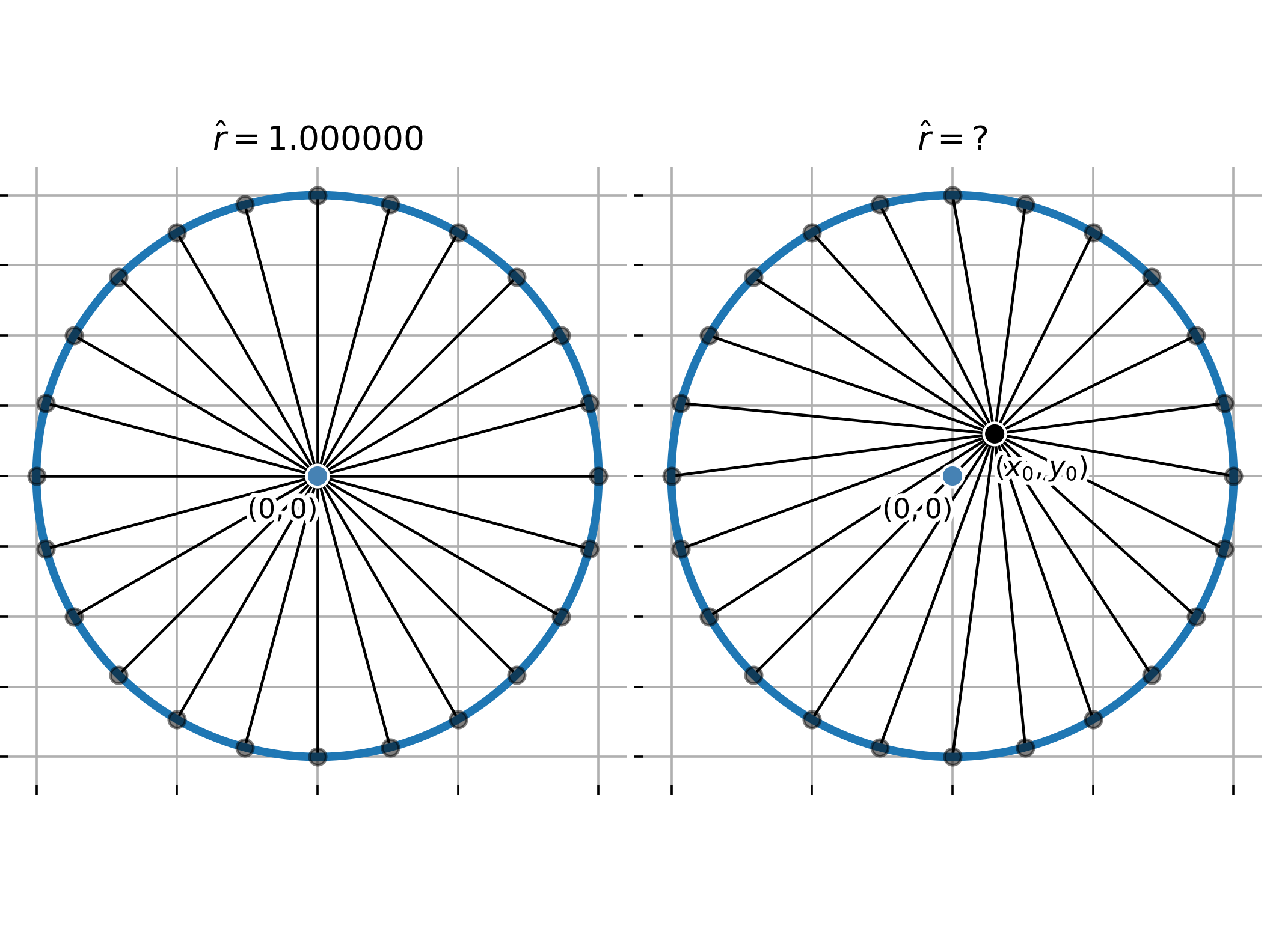
To demonstrate this, let's look at some sample measurements on the unit circle (which has a radius $r=1$ and center of $(0,0)$). I'll choose the off-center point $(x_0,y_0)=(.25,.15)$ and plot $n$ equidistant points on the circle's circumference:
To approximate the average off-center radius for the above circles, we can simply take the mean of the distances from $(x_0,y_0)$ to each of the $n$ points.
Each point on the unit circle is given by $(\cos(\theta), \sin(\theta))$, where $\theta$ is the angle (in this post, in radians) counterclockwise from the horizontal line $y=0$. Because there are $n$ points, the angle between each point is simply $\theta=\frac{2\pi}{n}$. Therefore, the $i$-th point is given by $\left(\cos(\theta i),\sin(\theta i)\right)$ if $i$ uses zero-based indexing.
To get the distance from one point on the circumference to our off-center point, we can use the Euclidean distance formula $d(\mathbf{p},\mathbf{q})=\sqrt{\sum_j{\left(\mathbf{q}_j-\mathbf{p}_j\right)^2}}$, where $\mathbf{q}$ is our point on the circumference $\mathbf{q}_i=\left(\cos(\theta i), \sin(\theta i) \right)$, and $\mathbf{p}$ is the off-center point $(x_0,y_0)$.
Therefore, each distance $d_i$ corresponding to the $i$-th point on the circumference is calculated as:
$$ d_i = \sqrt{\left(\cos(\theta i) - x_0\right)^2 + \left(\sin(\theta i) - y_0 \right)^2}, $$and the average off-center radius $\hat{r}$ is the arithmetic mean of these distances:
$$ \hat{r} = \frac{1}{n} \sum_{i=0}^{n-1}{\sqrt{\left(\cos(\theta i) - x_0\right)^2 + \left(\sin(\theta i) - y_0 \right)^2}} $$This is visualized for the same off-center point $(.25, .15)$ below:
As we increase the number of measurements to the circumference $n$, we also decrease the angle between these lines, $\theta$, and yield a closer approximation to the average radius $\hat{r}$.
We can visualize how approximations of $\hat{r}$ change as $n$ increases and $(x_0,y_0)$ changes:
We see that for low $n$, the distribution of $\hat{r}$ is biased in certain locations due to the proximity to the equidistant sampled points. For larger $n$, these artifacts start to fade, yielding a smoother distribution of $\hat{r}$.
However, what we'd really like is the value of $\hat{r}$ as we increase the number of measured distances infinitely, or as $n\to\infty$ (equivalently, $\theta\to0$). As any keen calculus student will tell you, adding up a bunch of terms that become smaller and smaller is analogous to an integral.
To take an integral with respect to $\theta$, we'll rephrase the summation by dropping the discrete $i$ term and normalizing by the total number of angles ($2\pi$) (you can think of this as averaging over all possible degrees of rotation of measuring from $(x_0,y_0)$ to the circumference):
$$ \hat{r} = \frac{1}{2\pi} \int_0^{2\pi}{\sqrt{\left(\cos(\theta) - x_0\right)^2 + \left(\sin(\theta) - y_0 \right)^2}}d\theta, $$and when evaluated at the center of the circle, $(x_0,y_0)=(0,0)$, we can show that the average radius is $1$ using the trigonometric identity $\sin^2\theta+\cos^2\theta=1$:
$$ \begin{align*} \hat{r} &= \frac{1}{2\pi} \int_0^{2\pi}{\sqrt{\left(\cos(\theta) - x_0\right)^2 + \left(\sin(\theta) - y_0 \right)^2}}d\theta \\ &= \frac{1}{2\pi} \int_0^{2\pi}{\sqrt{\left(\cos(\theta) - 0\right)^2 + \left(\sin(\theta) - 0 \right)^2}}d\theta \\ &= \frac{1}{2\pi} \int_0^{2\pi}{1}d\theta \\ &= \frac{1}{2\pi} \theta\bigg|_0^{2\pi} \\ &= \frac{1}{2\pi} 2\pi \\ &= 1 \end{align*} $$In Python, this can be written as:
def r_int(x0=0, y0=0):
f = lambda t : np.sqrt((np.cos(t)-x0)**2 + (np.sin(t)-y0)**2)
return scipy.integrate.quad(f, 0, 2*np.pi)[0]/(2*np.pi)
where at $(x_0,y_0)=(0,0)$ we obtain the expected result:
r_int()
If we compare this analytical solution to our approximations as $(x_0,y_0)$ becomes farther from the origin, we can visualize the alignment as $n$ increases (note that the circle heat maps above are superfluous due to circular symmetry):
Evidently, both the analytical and numerical solutions agree that $\hat{r}>1$, but it's not clear why that's the case. One way to explain this is by visualizing the areas within the circle that result in distances to the off-center point both less than and greater than the true radius (in this case, 1).
If we fix $y=0$ and vary $x$ to be far from the origin, we can visualize which points on the circumference lead to certain magnitudes of distance:
By drawing another unit circle about the off-center point (right) in reference to the original unit circle (left), we can clearly see the points which have a maximum distance of 1 (red) and those that are farther away (blue).
Shading in these areas demonstrates how the blue portion (where distances are greater than 1) is substantially larger than the red:
And when we normalize these areas by their angles, it becomes clear why the average off-center radius is larger than 1: The following plot shows how the normalized areas increase and decrease as we move this off-center point away from $x=0$:
Crucially, the normalized blue area increases much faster than the normalized red area decreases. This tells us that as the off-center point moves farther from the origin, the count and magnitude of distances greater than 1 outnumber those that are less than 1.
Indeed, a transformation of these two areas closely approximates $\hat{r}$, shown above in orange.
Therefore, we can solve for their points of intersection: The $x$ coordinate is given when $$ (x-x_0)^2+(1-x^2)=1\\ \implies x^2-2x_0x+x_0^2-x^2=0 \\ \implies x_0^2 = 2x_0x \\ \implies x = \frac{x_0}{2} $$ The $y$ coordinates can be retrieved by plugging this into the unit circle's formula: $$ \left(\frac{x_0}{2}\right)^2+y^2 = 1 \\ \implies 4y^2 = 4 - x_0^2 \\ \implies y = \pm \frac{1}{2}\sqrt{4-x_0^2} $$ Therefore, the base of the isosceles triangle is $\sqrt{4-x_0^2}$, and the height is simply $x_0-\frac{x_0}{2}=\frac{x_0}{2}$. This means the area of the triangle is: \begin{align*} A_1&=\frac{1}{2}\cdot\sqrt{4-x_0^2}\cdot\frac{x_0}{2} \\ &= \frac{x_0\sqrt{4-x_0^2}}{4} \end{align*} The area of an ellipsis is $\pi\cdot r_1 \cdot r_2$ where $r_1,r_2$ are the two axes. We know that $r_1=\frac{1}{2}\sqrt{4-x_0^2}$ due to the $y$-intersect, and we also know $r_2$ stretches from the end of the left circle ($x=1$) to its intersection ($x=\frac{x_0}{2}$). Therefore, $r_2=1-\frac{x_0}{2}=\frac{2-x_0}{2}$. Knowing this, we can calculate the halved area of the ellipsis: \begin{align*} A_2 &= \frac{1}{2} \left(\pi \cdot \frac{\sqrt{4-x_0^2}}{2} \cdot \frac{2-x_0}{2} \right) \\ &= \frac{\pi\sqrt{4-x_0^2}(2-x_0)}{8} \end{align*} The red area $R$ is thus given by subtracting the triangle's area from the ellipse's: \begin{align*} R &= A_2 - A_1 \\ &= \frac{\sqrt{4-x_0^2}\cdot\pi(2-x_0)}{8} - \frac{x_0\sqrt{4-x_0^2}}{4} \\ &= \frac{\sqrt{4-x_0^2}\cdot\pi(2-x_0) - 2x_0\sqrt{4-x_0^2}}{8} \\ &= \frac{\sqrt{4-x_0^2}(\pi(2-x_0) - 2x_0)}{8} \end{align*} Since the area of the unit circle is $\pi(1)^2=\pi$, the blue area is simply $B=\pi-R$. To normalize both areas, we will divide by the angles corresponding to each area. Re-examining the intersections of the two circles, there is an isosceles triangle created from $(x_0,0)$ to $(x_0/2, \sqrt{4-x_0^2})$ (the positive $y$-intersect), and $(0,0)$ with side lengths 1, 1, and $x_0$.
The right-most angle of this triangle is $\cos^{-1}\left(\frac{x_0}{2}\right)$, meaning the angle in the blue sector is twice this, $2\cos^{-1}\left(\frac{x_0}{2}\right)$, and complementary for the red area, $2\pi-2\cos^{-1}\left(\frac{x_0}{2}\right)$. Ultimately, the normalized areas are: $$ R^\prime = \frac{\sqrt{4-x_0^2}(\pi(2-x_0) - 2x_0)}{16(\pi-\cos^{-1}(x_0/2))},\quad B^\prime = \frac{8\pi - \sqrt{4-x_0^2}(\pi(2-x_0) - 2x_0)}{16\cos^{-1}(x_0/2)} $$ For reasons that are not entirely clear to me, the transformation $$ \frac{R'+B'}{\pi/2} $$ produces a curve that resembles $\hat{r}$ (plotted above) but with a $y$-intercept of $2/\pi$ (since $R'+B'=1$ at $x_0=0$). Shifting the curve up by the required amount, $(\pi-2)/\pi$, yields the orange line.
The average off-center diameter is always less than the true diameter¶
You might think that since the average off-center radius is always larger than 1, the average off-center diameter must be greater than 2, since the diameter is twice the radius—but you'd be wrong! This becomes clear with a visualisation:
Here, the dashed blue line is the true diameter drawn at an angle $\theta$ counterclockwise from the horizontal axis, which passes through the origin by definition. The solid black line is parallel to this plotted diameter, and is evidently shorter than the length of the true diameter due to the curvature of the circle.
If you imagine rotating this solid black line around the entire circle (thus varying $\theta$) and taking measurements in order to derive the average off-center diameter, you can see how each measurement would be strictly less than the true diameter, except for one—the line that passes through the origin (shown in solid blue below):
plot_diameter(.25, .15, theta=55, show_diameter=True)
Since all other lengths about the off-center point are strictly smaller than the diameter, taking the mean therefore yields an average off-center diameter strictly smaller than 2.
To conclude this blog post, I'll formulate a closed-form solution for the average off-center diameter to show how its value changes as we conduct a similar exercise of choosing an off-center point progressively farther from the center ($x\to1$).
First, for some $\theta$ pictured above, we have the straight line:
The gradient of this line is $\frac{\Delta y}{\Delta x}$, which is the same as $\tan \theta$. To find the $y$-intercept of this line, we can plug in $(x_0,y_0)$ since the point must lie on the line:
$$ \begin{align*} y&=x\cdot\tan\theta + \beta \\ \implies y_0&=x_0\tan\theta+\beta \\ \implies \beta&=y_0-x_0\tan\theta, \end{align*} $$so the final formula for the line is
$$ \begin{align} y=x\cdot\tan\theta+\left(y_0-x_0\cdot\tan\theta\right) \end{align} $$The length of this line enclosed by the unit circle is just the distance between the two points of intersection with the unit circle. Since we know the unit circle is given by $x^2+y^2=1$, we can solve for these points, starting with $x$ (I will use $\beta$ to represent the $y$-intercept for brevity):
$$ \begin{align*} \sqrt{1-x^2} &= x\cdot\tan\theta + \beta \\ 1 - x^2 &= x^2\cdot\tan^2\theta + 2x\beta\cdot\tan\theta + \beta^2 \\ 0 &= 1 - \beta^2 - 2x\beta\cdot\tan\theta + x^2\left(-\tan^2\theta-1\right) \\ &= x^2 - \frac{2\beta\cdot\tan\theta}{-\tan^2\theta-1}x + \frac{-\beta^2+1}{-\tan^2\theta-1} \end{align*} $$this is a quadratic equation which we can solve using the quadratic formula:
$$ x = \frac{\pm\sqrt{-4\beta^2 + 4\tan^2(\theta)+4}-2\beta\tan(\theta)}{2\left(\tan^2(\theta)+1\right)} $$and thus
$$ y = \frac{\pm\sqrt{-4\beta^2 + 4\tan^2(\theta)+4}-2\beta\tan(\theta)}{2\left(\tan^2(\theta)+1\right)}\tan(\theta) + \beta $$In total, we have two points $(x_1,y_1)$ and $(x_2,y_2)$ which we can compute the distance between, which is the off-center diameter at a given theta, $\hat{d}_\theta$ (note that expanded forms are largely omitted here since it gets very messy, very quickly).
$$ \begin{align*} \hat{d}_\theta &= \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2} \\ &= \cdots \\ &= \sqrt{\left(-4 \cos^2(\theta)\left(\beta^2 \cos^2(\theta) - 1\right)\right) + \left(-4 \sin^2(\theta) \left(\beta^2 \cos^2(\theta) - 1\right)\right)} \\ &= \sqrt{4-4\beta^2\cos^2(\theta)} \\ &= \sqrt{4-4\left(y_0-x_0\tan\theta\right)^2\cos^2(\theta)} \end{align*} $$Let's do some sanity checking by plugging in the origin—we know this should give us $\hat{d}_\theta=2$ for any $\theta$:
$$ \begin{align*} \hat{d}_\theta &= \sqrt{4-4\left(0-0\tan\theta\right)^2\cos^2(\theta)} \\ &= \sqrt{4-4\cdot0^2\cdot\cos^2(\theta)} \\ &= \sqrt{4} \\ &= 2 \end{align*} $$Now, converting our single-angle expression to an integral, we have:
$$ \hat{d} = \frac{1}{\pi} \int_0^\pi {\sqrt{4-4\left(y_0-x_0\tan\theta\right)^2\cos^2(\theta)}} d\theta $$Here we only need to average over $\pi$ since the line between opposite points on the circumference at the angle $\theta$ is the same as the angle $\pi+\theta$, and we don't want to double-count distances.
Sanity checking this formulation for $(x_0, y_0) = (0,0)$, we've shown that the integrand is $2$ above, so the average off-center diameter is:
$$ \begin{align*} \hat{d} &= \frac{1}{\pi} 2\theta\bigg|_0^\pi \\ &= \frac{1}{\pi} 2\pi \\ &= 2 \end{align*} $$Similar to the average radius, we can define this as a Python function:
def d_int(x0=0, y0=0):
f = lambda t : np.sqrt(4 - 4*(y0 - x0*np.tan(t))**2*np.cos(t)**2)
return scipy.integrate.quad(f, 0, np.pi)[0]/(np.pi)
d_int()
And we can visualize how the average diameter changes as $x\to1$: