While I have obtained permission to use the question publicly, I have slightly altered and reworded the problem. All credit for the question is attributed to the wonderful Prof. Julián García. Here it is:

Say we have a game with three players: $A$, $B$, $C$.
Starting with $A$, each player rolls an $n$-sided die once and then passes the die to the next player.
The first player to roll a $1$ wins the game.
For example, if $B$ wins on the second round, the sequence would be: $A, B, C, A, B$.

What is the probability of each player winning?

Not necessarily a difficult problem, and I encourage you to have a go — but it is fun to play around with.

Analytical solution #1 — Direct¶

First, let's take a moment to ponder what the result should look like. By intuition, if we note that this is a cyclic game of chance, it would make sense to say that those who take turns before others naturally have an advantage. Since $A$ goes before $B$ and $B$ goes before $C$, it stands to reason that $\mathbb{P}(A \text{ wins}) \gt \mathbb{P}(B \text{ wins}) \gt \mathbb{P}(C \text{ wins})$ might be true. We'll keep this in mind moving forward as a sanity check.

We can start by visualizing a game: $$\begin{matrix} \text{turn } t & 1 & 2 & 3 & 4 & 5 & 6 & 7 & \space \\ \text{player} & A & B & C & A & B & C & A & \dots \end{matrix}$$ With $t$ denoting a turn, a 'round' denoting a set of three turns beginning with $A$, and $\mathbb{P}(X)$ denoting the probability of player $X$ winning the game.

It's worth stating that players can win at multiple $t$, meaning we're going to be dealing with a sum. For example, for $A$ to win, a $1$ could be rolled on the first turn ($t=1$), with probability $\frac{1}{n}$.

Alternatively, $A$ could win during the second round at $t=4$. For this to happen, the first three turns must not result in a win (i.e., not roll a $1$), and then $A$ must roll a $1$. This occurs with probability $$\frac{n-1}{n}\cdot\frac{n-1}{n}\cdot\frac{n-1}{n}\cdot\frac{1}{n} = \left(\frac{n-1}{n}\right)^3 \cdot \frac{1}{n}$$

$A$ could also win at $t=7$ or $t=10$ or $t=13$ or et cetera. It's pretty clear where this is heading. We can express this as

$$P(A)=\left(\frac{1}{n}\right) + \left(\left(\frac{n-1}{n}\right)^3 \cdot \frac{1}{n}\right) + \left(\left(\frac{n-1}{n}\right)^6 \cdot \frac{1}{n}\right) + \dots $$

Note that $A$ can only win at the start of some new round, which is some multiple of $3$ turns ($0$ included) followed by rolling a $1$. We must first lose some number of rounds and then win one. The probability of $A$ winning at some round $k$ where we index $k$ starting at zero ($k\in\{0,1,2,\dots\}$) is thus: $$\mathbb{P}(A_k) = \left(\frac{n-1}{n}\right)^{3k} \cdot \frac{1}{n}$$

Theoretically, these games could last for a long time (i.e., an arbitrarily large amount of rounds). So, we need to account for every possible $k$ producing a nonzero value in $\mathbb{P}(A_k)$. We can call this $\mathcal{K}$. To obtain $\mathbb{P}(A)$, we need to therefore sum over each $k\in\mathcal{K}$, or every round in the support of $\mathbb{P}(A_k)$, leaving us with

$$\mathbb{P}(A) = \sum_{k\in\mathcal{K}}\left(\left(\frac{n-1}{n}\right)^{3k} \cdot \frac{1}{n}\right)$$

Since there is a nonzero probability of terminating at an arbitrarily large round, we can equivalently write:

$$\mathbb{P}(A) = \sum_{k=0}^\infty\left(\left(\frac{n-1}{n}\right)^{3k} \cdot \frac{1}{n}\right)$$

For $\mathbb{P}(B)$, $\mathbb{P}(C)$, the win condition is essentially identical to $\mathbb{P}(A)$, just shifted either one or two turns to the right for $B$ and $C$ respectively. In other words, for any winning round $k$, $B$'s number of losses is $t=3k+1$, and $C$'s is $t=3k+2$. Now we have our analytical probabilities:

$$ \begin{align} \mathbb{P}(A) &= \sum_{k=0}^{\infty}{\left(\left(\frac{n-1}{n}\right)^{3k}\cdot\frac{1}{n}\right)} \\ \mathbb{P}(B) &= \sum_{k=0}^{\infty}{\left(\left(\frac{n-1}{n}\right)^{3k+1}\cdot\frac{1}{n}\right)} \\ \mathbb{P}(C) &= \sum_{k=0}^{\infty}{\left(\left(\frac{n-1}{n}\right)^{3k+2}\cdot\frac{1}{n}\right)} \end{align} $$

While these sums look intimidating, they can actually be converted to closed-form solutions rather easily. This is because each sum is just a bloated geometric series.

If we let $\alpha=\left(\frac{n-1}{n}\right)$ and $\beta=\frac{1}{n}$, then we can rewrite

$$ \mathbb{P}(A) = \sum_{k=0}^{\infty}\left[\left(\frac{n-1}{n}\right)^{3k}\cdot\frac{1}{n}\right] = \sum_{k=0}^\infty\left(\alpha^{3k}\cdot\beta\right) = \beta\sum_{k=0}^\infty \alpha^{3k} $$

Keeping in mind $n$ (and thus $\beta$) is a constant, we're now only concerned with $\sum_{k=0}^\infty \alpha^{3k} $.

The sum $S$ of an infinite geometric series is given by $$ S = \frac{a_0}{(1-r)} $$ where $a_0$ is the first term of the series and $r$ is the common ratio.

The first term is just

$$ a_0 = \left(\frac{n-1}{n}\right)^{3(0)} = 1 $$

and the common ratio is

$$ r = \frac{a_1}{a_0} = a_1 = \frac{(n-1)^3}{n^3} $$

So we can easily solve for $S$ as below:

$$ \begin{align} S = \frac{a_0}{(1-r)} &= \frac{1}{\left(1-\frac{(n-1)^3}{n^3}\right)} \\ &= \frac{n^3}{n^3 - (n-1)^3} \\ &= \frac{n^3}{3n^2 - 3n + 1} \end{align} $$

And recall that

$$ \mathbb{P}(A) = \beta\sum_{k=0}^\infty \alpha^{3k} $$

and thus

$$ \mathbb{P}(A) = \frac{n^2}{3n^2 - 3n + 1} $$

We can similarly compute the closed-form summation for other players to find

$$ \begin{align} \mathbb{P}(B) &= \frac{n(n-1)}{3n^2 - 3n + 1} \\ \mathbb{P}(C) &= \frac{(n-1)^2}{3n^2 - 3n + 1} \end{align} $$

You'll notice that all solutions have the same denominator, as a result of their similarity of forms as sums. This is also where we can conduct our sanity check from the beginning:

$$ \mathbb{P}(A) \stackrel{?}{\gt} \mathbb{P}(B) \stackrel{?}{\gt} \mathbb{P}(C) $$

And if we look at our results, we can see that

$$ n^2 \gt n(n-1) \gt (n-1)^2 $$

for $n>1$, so we can be a little more confident in our answer.

Analyzing the game¶

Now we have the three functions, let's figure out the probabilities for each player for a regular $6$-sided die. Evaluating each function, we find that:

$$ \begin{align} \mathbb{P}(A) &\approx 0.396 \\ \mathbb{P}(B) &\approx 0.330 \\ \mathbb{P}(C) &\approx 0.275 \end{align} $$

So compared to $A$, $B$ is approximately $6.6\%$ less likely to win, and $C$ around $12.1\%$.

So we've sort of answered the question at hand, but we haven't played with $n$ (faces on the die) yet, which is a parameter we can control. Let's see how the probabilities of each player winning change as we manipulate $n$.

We can start by calculating the probabilities for $2\le n \le 24$:

And then plot how the win rates differ:

Which shows us that as $n\to\infty$, $\mathbb{P}(A)$, $\mathbb{P}(B)$, and $\mathbb{P}(C)$ seem to be converging to equal values. In fact, we can show that

$$ \lim_{n\to\infty}\left\{ \frac{n^2}{n^3-(n-1)^3} \right\} = \lim_{n\to\infty}\left\{ \frac{n(n-1)}{n^3-(n-1)^3} \right\} = \lim_{n\to\infty}\left\{ \frac{(n-1)^2}{n^3-(n-1)^3} \right\} = \frac{1}{3} $$

by some algebra and L'Hôpital's rule.

In other words, with an arbitrarily large amount of faces on a die, we produce a fair game.

And the fun part is, this is actually quite explainable: with fewer number of sides on a die (small $n$), the probability of rolling a $1$ is not too rare (say, $\frac{1}{6}$ for a normal die). Naturally, this means whoever rolls first also has a higher chance of rolling the $1$ first (note that for smaller $n$, $\frac{1}{n}\gt \left(\frac{n-1}{n}\right)^k \cdot \frac{1}{n}$ for $k\ge1$). This is why $A$ has an advantage for smaller $n$.

However, as the number of sides on the die increases, rolling a $1$ on the first try or at all becomes a lot more rare. So, the probability gets spread thin across all three players, and approaches a uniform distribution such that in the long run, $\mathbb{P}(A) = \mathbb{P}(B) = \mathbb{P}(C)$.

Another interesting observation is that as $n$ grows, $\mathbb{P}(B)$ does not change as drastically as $\mathbb{P}(C)$, which itself does not change as drastically as $\mathbb{P}(A)$. Rather, the probability shifts from $A$ to $C$, with $B$ acting almost like a 'channel' of probability flow. An intuitive but informal way to frame this is that $A$ holds the biggest advantage and $C$ holds the biggest disadvantage, whereas $B$ is more neutral as the middle player, so its gains of an increased $n$ are marginal by comparison.

Analytical solution #2 — Markov chain¶

This section covers another analytical approach to the problem — and while I think it's another intuitive pathway to a solution, feel free to skip to the the simulation method if you're uninterested.

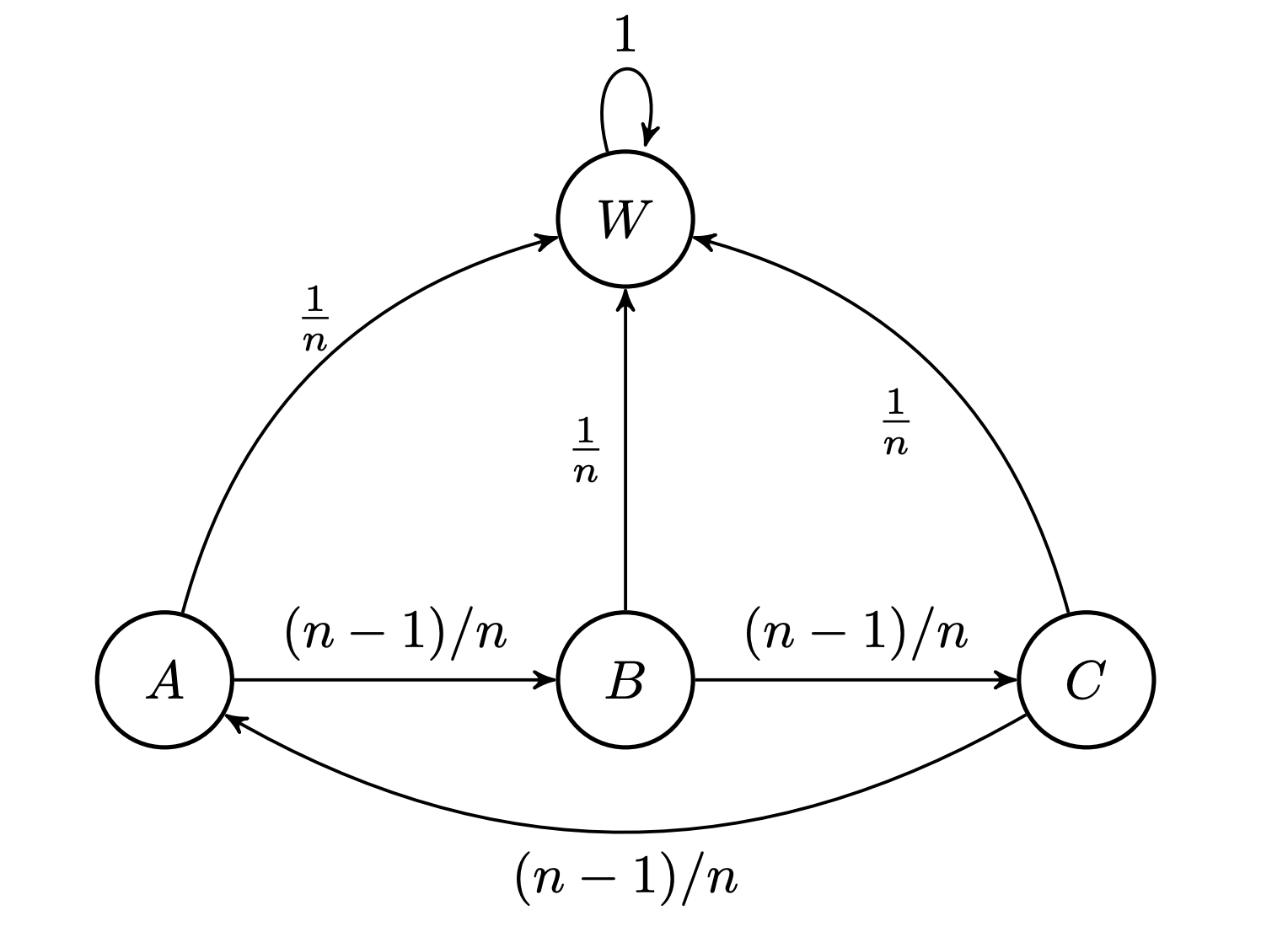
You may have noticed the game can be framed as a Markov chain, like so:

Of course, the stochastic process only encompasses our game if we begin the process with player $A$, or at state $A$ (but not really, because the states are arbitrary names, with equal probabilities — more on this later). A 'win' state $W$ has been added to the chain to signify someone has rolled a $1$. Personally, the above graphic makes the game a touch easier to understand, and actually feels a little more natural to visualize, compared to the direct approach.

If you're unfamiliar with Markov chains, just imagine a process where with each increase in $t$, given that you're in one state (or 'node'), you must transition to any connected state in the next turn ($t+1$) with an associated probability. These probabilities and states can be described by a non-graphic representation called the transition matrix $\mathbf{P}$, which is essentially a collection of probability distributions regarding transitions to the state at turn $t+1$, given a current state at turn $t$.

You may also notice that this is an absorbing Markov chain, meaning every state (or every player) can reach an 'absorbing' state, in this case $W$. It's called an absorbing state because it has a probability of $1$ to transition to itself, here we're interpreting the absorption as a win condition.

We can employ some commonly used methods for long-term behavior of an absorbing Markov chain to try to find our probabilities. Reusing variables $\alpha$ and $\beta$ from before, we can describe the transition matrix as

$$ \mathbf{P} = \begin{array}{ c | c c c c } & A & B & C & W \\ \hline A & 0 & \alpha & 0 & \beta \\ B & 0 & 0 & \alpha & \beta \\ C & \alpha & 0 & 0 & \beta \\ W & 0 & 0 & 0 & 1 \end{array} $$

Such that $\mathbf{P}_{ij}$ (the $i$-th row and $j$-th column of $\mathbf{P}$) denotes the probability of transition from state $i$ to state $j$.

We can then arrange $\mathbf{P}$ to be in what is known as canonical form, where the matrix is arranged such that it can be sectioned into the following form:

$$ \mathbf{P} = \left( \begin{array}{ c | c } \mathbf{Q} & \mathbf{R} \\ \hline \mathbf{0} & \mathbf{I} \end{array} \right) $$

Such that $\mathbf{Q}$ is the matrix denoting transitions between only transient (non-absorbing) states, $\mathbf{R}$ is the matrix denoting transitions between transient states to absorbing states, and $\mathbf{I}$ is the identity matrix. If we look at our above matrix for the specified problem, it is actually already in this configuration, so we don't need to re-organise it.

Using the canonical form, we can compute what is called the fundamental matrix $\mathbf{N}$, in which each entry $\mathbf{N}_{ij}$ tells us the expected number of visits to a transient state $j$ starting from state $i$ before absorption. The fundamental matrix is actually a matrix of a geometric series (but with a closed-form solution), so in a sense I'm cheating by considering this a 'different' approach, but the method is entertaining nonetheless.

The fundamental matrix is given by $\mathbf{N}=(\mathbf{I}-\mathbf{Q})^{-1}$, so we can compute it as follows:

$$ \begin{align} \mathbf{N} &= \left[\left( \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right) - \left( \begin{matrix} 0 & \alpha & 0 \\ 0 & 0 & \alpha \\ \alpha & 0 & 0 \end{matrix} \right) \right]^{-1} \\ &= \left( \begin{matrix} 1 & -\alpha & 0 \\ 0 & 1 & -\alpha \\ -\alpha & 0 & 1 \end{matrix} \right)^{-1} \end{align} $$

Which is solvable via the Gauss-Jordan algorithm

$$ \begin{align} &\left( \begin{array}{c c c | c c c} 1 & -\alpha & 0 & 1 & 0 & 0 \\ 0 & 1 & -\alpha & 0 & 1 & 0 \\ -\alpha & 0 & 1 & 0 & 0 & 1 \end{array} \right) \xrightarrow{R_3\leftarrow R_3 + \alpha\cdot R_1} \left( \begin{array}{c c c | c c c} 1 & -\alpha & 0 & 1 & 0 & 0 \\ 0 & 1 & -\alpha & 0 & 1 & 0 \\ 0 & -\alpha^2 & 1 & \alpha & 0 & 1 \end{array} \right) \\ \xrightarrow{R_3\leftarrow \alpha^2 R_2 + R_3} &\left( \begin{array}{c c c | c c c} 1 & -\alpha & 0 & 1 & 0 & 0 \\ 0 & 1 & -\alpha & 0 & 1 & 0 \\ 0 & 0 & 1-\alpha^3 & \alpha & \alpha^2 & 1 \end{array} \right)\\ \xrightarrow{\dots} &\left( \begin{array}{c c c | c c c} 1 & 0 & 0 & \frac{1}{1-\alpha^3} & \frac{\alpha}{1-\alpha^3} & \frac{\alpha^2}{1-\alpha^3} \\ 0 & 1 & 0 & \frac{\alpha^2}{1-\alpha^3} & \frac{1}{1-\alpha^3} & \frac{\alpha}{1-\alpha^3} \\ 0 & 0 & 1 & \frac{\alpha}{1-\alpha^3} & \frac{\alpha^2}{1-\alpha^3} & \frac{1}{1-\alpha^3} \end{array} \right) \end{align} $$

So now we have

$$ \mathbf{N}= \left( \begin{matrix} \frac{1}{1-\alpha^3} & \frac{\alpha}{1-\alpha^3} & \frac{\alpha^2}{1-\alpha^3} \\ \frac{\alpha^2}{1-\alpha^3} & \frac{1}{1-\alpha^3} & \frac{\alpha}{1-\alpha^3} \\ \frac{\alpha}{1-\alpha^3} & \frac{\alpha^2}{1-\alpha^3} & \frac{1}{1-\alpha^3} \end{matrix} \right) $$

Remember, the interpretation of $\mathbf{N}_{ij}$ is the expected number of times state $j$ is visited starting in state $i$ before absorption. So, we are actually only interested in information regarding starting in state $A$ (i.e., the top row — but regardless note the shift of the row $1$ pattern in rows $2$ and $3$ to the right, because states have identical probabilities, so it functionally doesn't matter what labelled state we choose to start from.)

If we sum the first row, we should attain the total number of expected states visited before absorption — or how long we expect a game to last. This is given by

$$ \begin{align} \frac{1 + \alpha + \alpha^2}{1-\alpha^3} &= \frac{1 + \alpha + \alpha^2}{-(\alpha-1)(1 + \alpha + \alpha^2)} \\ &=\frac{1}{1-\alpha} \\ &=\frac{1}{1-\frac{n-1}{n}} \\ &=n \end{align} $$

This is... kind of beautiful. It tells us that with an $n$-sided die, we should expect the average game to last $n$ turns until we roll a $1$.

With this information, we can now derive $\mathbb{P}(A)$, $\mathbb{P}(B)$, and $\mathbb{P}(C)$. If we know the total expected number of times we visit states in an average game, and we know the number of times we expect to visit an individual state, and we note that more time spent in a state means we win more often in that state, then the average (or long run) probabilities for each player are simply the proportions of time spent in that state relative to the total time, given that we start in state $A$.

I'll leave it to you to do the algebra, but if we normalize each $\mathbf{N}_{Aj}$ by the total expected number of turns $n$, we achieve:

$$ \begin{align} \mathbb{P}(A) &= \frac{1}{(1-\alpha^3)\cdot n} = \frac{n^2}{3n^2-3n+1} \\ \mathbb{P}(B) &= \frac{\alpha}{(1-\alpha^3)\cdot n} = \frac{n(n-1)}{3n^2 - 3n + 1} \\ \mathbb{P}(C) &= \frac{\alpha^2}{(1-\alpha^3)\cdot n} = \frac{(n-1)^2}{3n^2 - 3n + 1} \end{align} $$

Which is identical to the probabilities obtained in the direct approach.

Simulation method¶

Often, we like to back up our analytical approaches with simulation that validates our analytical models. Perhaps the discovery that the average game length is $n$ turns may be cause for a raised eyebrow, or maybe you just don't trust either analytical approach — so we want to simulate the game.

We could simulate the Markov chain (MCMC), but this would assume the transition matrix is correct, and because we might want to create an approach indpendent of the analytical one, we'll simulate the entire game instead. Each game with a certain $n$ will be played some number of times, and we'll aggregate the simulated data to approximate the probabilities of winning. This method of simulation is commonly referred to as the Monte Carlo method.

The above Python code describes the game pretty much verbatim; we repeat simulations for each game by cycling through players until someone rolls a $1$, and record who won the game and in how many turns.

Let's try calculating probabilities for $n=6$:

With $1\times 10^6$ simulated games, this is pretty close to the analytical approach — in terms of probabilities and average game length.

We can even compare performance to the analytical model as $n$ grows:

By eye, the Monte Carlo method proves pretty much indistinguishable from the analytical solution excepting some trouble in $\mathbb{P}(B)$. This is explained by the change in $\mathbb{P}(B)$ as $n\to\infty$ being much smaller than either $\mathbb{P}(A)$ or $\mathbb{P}(C)$ (note the ranges of axes), so the Monte Carlo averages just can't keep up with the level of precision $\mathbb{P}(B)$ warrants.

Something important to note is just how easy simulating the game was. The Python code is intuitive and simple, and all we had to do was sit back and let the process run to compute our statistics. We calculated empirical probabilities from simulated data and trusted its variance was low because of the sheer number of trials we ran. These are clear advantages of simulation methods. Indeed, if our problem was much more complex or had a significantly more convoluted rule set, perhaps the only feasible way we could analyze the problem would be through simulation.

Of course, the tradeoff is: with simulated data and empirical probabilities, we can only approximate values and suspect properties of the problem; we cannot deduce aspects for certain. Sometimes it is satisfying to prove these properties: for example, how games are expected to last exactly $n$ turns, or the fact that $\mathbb{P}(A)$, $\mathbb{P}(B)$, and $\mathbb{P}(C)$ all approach $\frac{1}{3}$ as $n\to\infty$.

This is, of course, just the surface of the discussion on analytical and simulation methods. In practice, a combination of the two is usually preferred to produce a more confident analysis.

Summary¶

In this post, I delved way too deep into a relatively simple probability theory question. I've offered two analytical approaches (out of who knows how many) and one simulation method to approach the same problem, with some discussion.

While I recognize the solutions I've employed are neither particularly insightful nor novel, I hope the exploratory factor was at least a little interesting. I also hope that you're now somewhat inspired to try out both simulation and analytical approaches in conjunction the next time you encounter an applicable problem.